Backpropagation and Automatic Differentiation

Gradient Descent

It’s a technique to solve the optimization problem of Empirical Risk Minimization which just means minimizing the average loss over our dataset. $\underset{x}{\min }\mathcal{L}(X,Y,w)=\frac{1}{N}{\sum }_{i=1}^N\ell (f(x_i;w),y_i)$

• $\ell$: loss for one sample (e.g. how wrong we are on one image)
• $\mathcal{L}$: average loss over all $N$ training examples
• $w$: model parameters (weights)

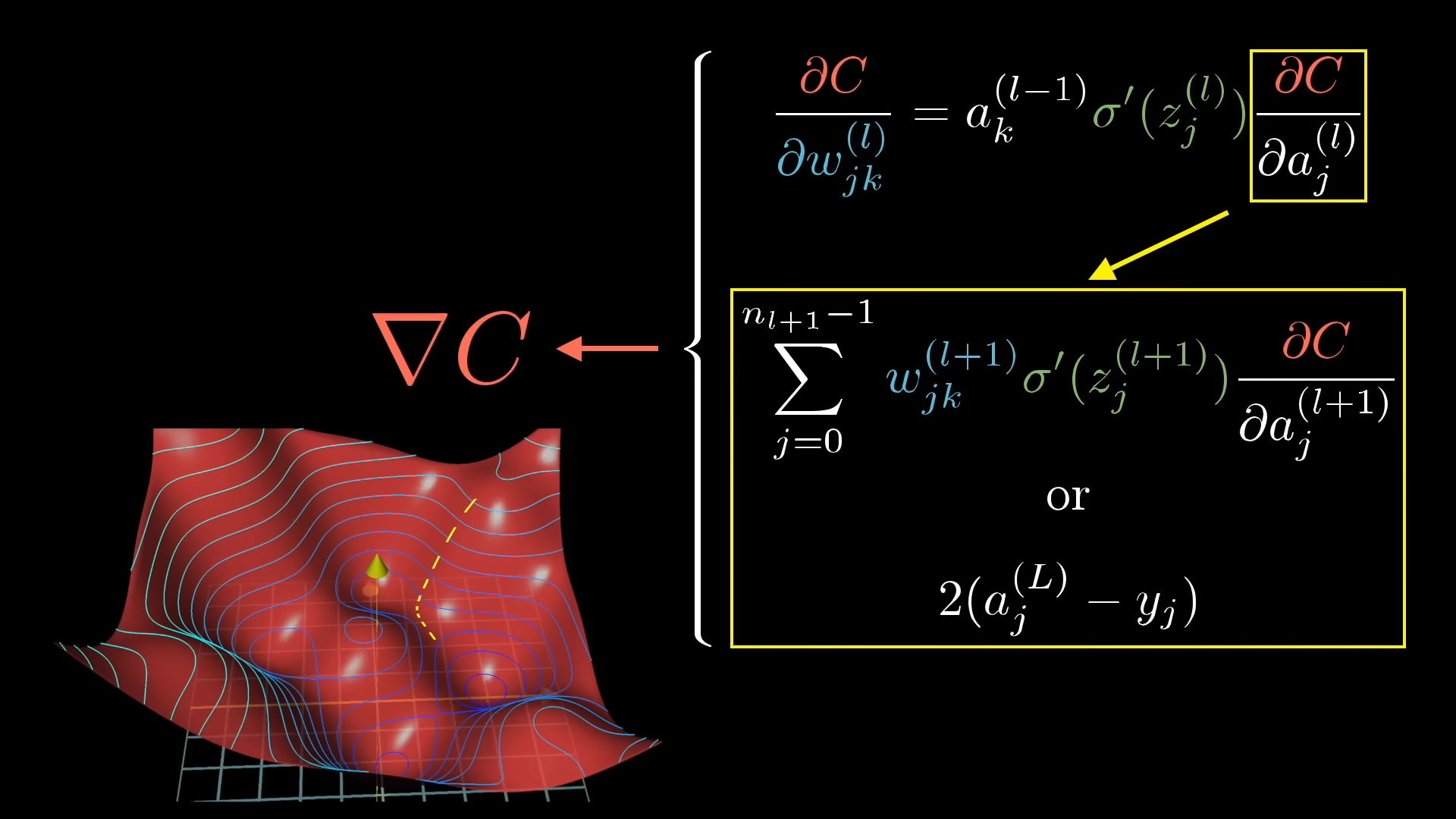
To minimize $\mathcal{L}$, we move the parameters $w$ a little bit in the direction that makes the loss decrease fastest, that direction is given by the negative gradient of the loss with respect to $w$. $w_{t+1}=w_t-{\nabla }_w\mathcal{L}(X,Y,w_t)$

• ${\nabla }_w\mathcal{L}$: vector of partial derivatives (how much each weight affects loss)
• $\alpha$: learning rate (step size)
• $t$: iteration number

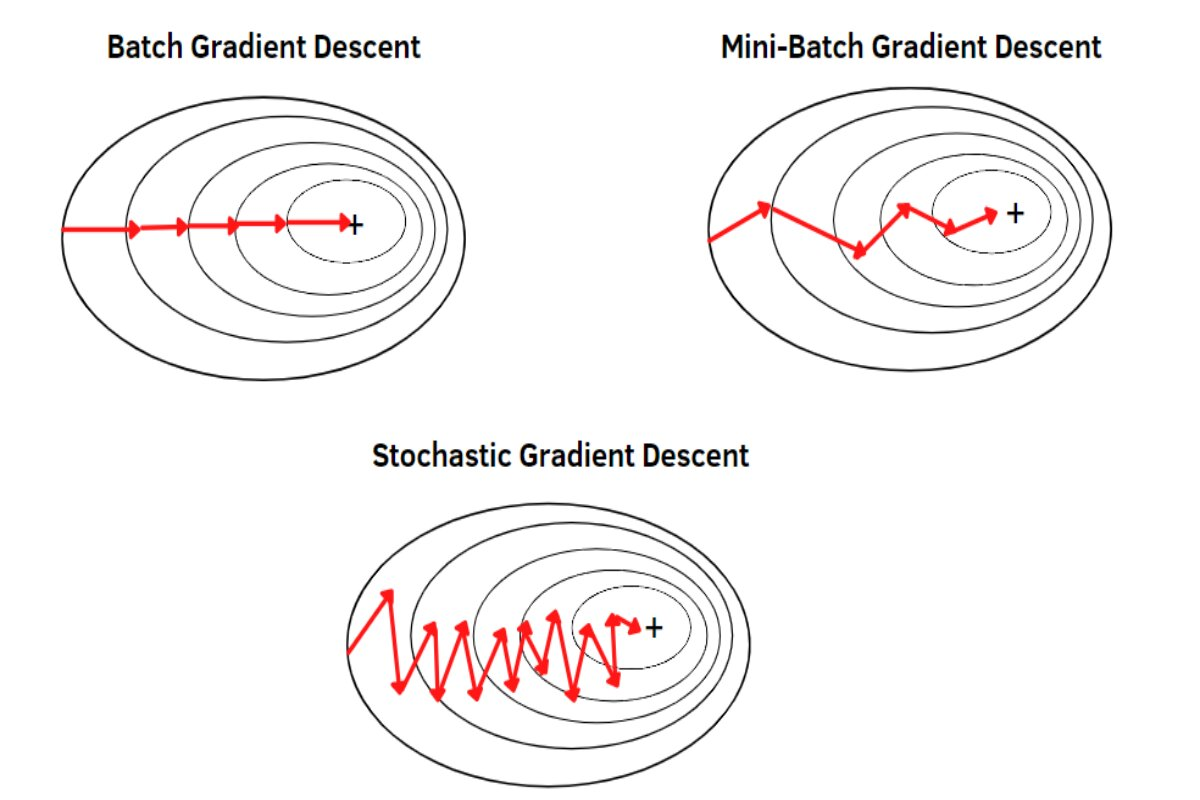
Gradient Descent Variants

• Batch (Full) Gradient Descent
  • Compute the gradient using the whole dataset
  • Precise but slow (need to pass through all samples before one update) (one update per epoch) ${\nabla }_w\mathcal{L}(X,Y,w)$
• Stochastic Gradient Descent
  • Compute the gradient using one sample at a time
  • Noisy but much faster, updates happen every time (one update per sample) ${\nabla }_w\ell (x_i,y_i,w)$
• Mini-Batch SDG
  • Compute the gradient on a small subset (e.g. 32 or 64 samples)
  • Faster than full batch, more stable than pure SDG (one update per batch) ${\nabla }_w\mathcal{L}(X_n,Y_n,w)$

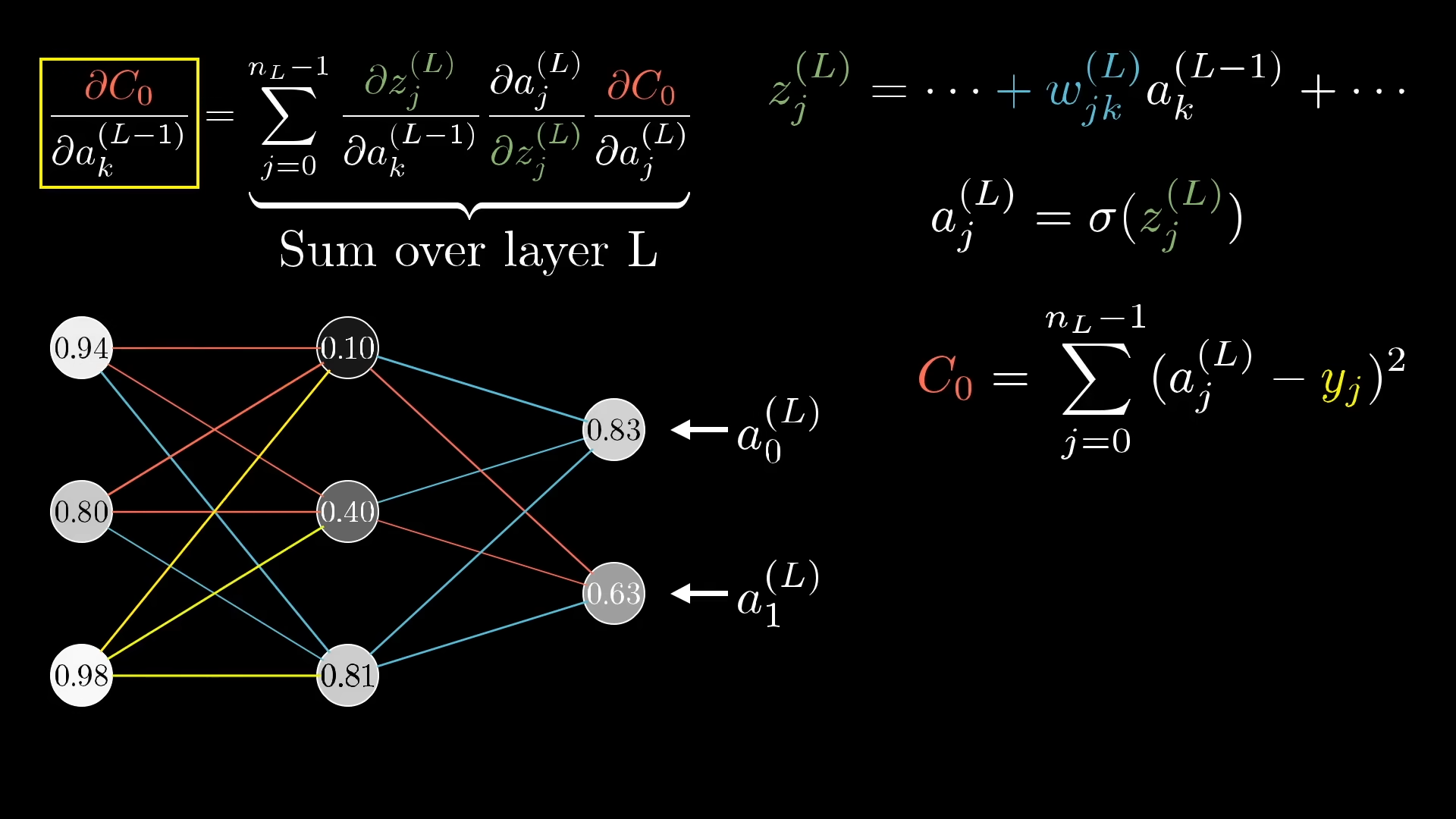
How to compute the gradient?

Finite difference requires $O(d)$ forward passes where $d$ is the number of parameters.

• Forward difference (1 forward pass per parameter) $\frac{\partial f}{\partial w_i}\approx \frac{f(w_i+\epsilon )-f(w_i)}{\epsilon }$
• Central difference (2 forward passes per parameter) $\frac{\partial f}{\partial w_i}\approx \frac{f(w_i+\epsilon )-f(w_i-\epsilon )}{2\epsilon }$

Automatic Differentiation

Much more efficient. $O(1)$ per layer. We compute derivatives exactly and efficiently by applying the chain rule programmatically.

• Forward-mode AD (compute derivatives and go forward)
• Reverse-mode AD (aka backpropagation)

PyTorch model

import torch
import torch.nn as nn
import torch.optim as optim
 
# Define model
class Net(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(784, 128)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(128, 10)
 
    def forward(self, x):
        x = self.relu(self.fc1(x))
        return self.fc2(x)
 
# Instantiate model, loss, optimizer
model = Net()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
 
# Training loop
for X, Y in dataloader:
    optimizer.zero_grad()
    outputs = model(X)
    loss = criterion(outputs, Y)
    loss.backward()   # <-- backprop (AD)
    optimizer.step()  # <-- gradient descent update